
a procedural programming language
Home | Overview | Download | Syntax | Math | Text | Code Samples | Forum | Contact
Code Samples
Procedures, Complex Arithmetic, Conditions I, and Loops
The procedure mandelbrot determines whether a point [x, y] in the complex domain is part of the famous Mandelbrot set by determining whether it leaves a certain radius after a given number of iterations.
| > mandelbrot := proc(x :: number, y :: number, iter)
:: number is > local c, z; > if unassigned(iter) then > iter := 128 > fi; > z := x!y; > c := z; > for i from 0 to iter while abs(z) < 2 do > z := z^2 + c > od; > return i > end; |
As can be seen in this example, the function firstchecks whether its first two arguments x and y are numbers. If the number of iterations iter has not been passed, the if unassigned .. statement sets the default to 128.
The procedure then converts the numbers x and y to the complex number z
(sixth line of the procedure), sets a fixed point c (seventh line), and
iterates z until either the
stop value iter is reached or the while condition abs(z) < 2
evaluates to false.
The number of iterations conducted is returned (last but one line of
the
procedure).
The point [0, 0] is part of the Mandelbrot set ...
| > mandelbrot(0, 0): 129 |
... even after 1024 iterations:
| > mandelbrot(0, 0, 1024): 1025 |
Conditions II and Error Handling
The next procedure demonstrates if-clauses as well as case of/else statements.
The procedure takes a numeric argument x and converts it to
degrees Celsius (assuming x is in degrees Fahrenheit) if the
second argument for rule is the character 'C', or converts it
to degrees Fahrenheit (assuming x is in
degrees Celsius) if the second argument is the character 'F' or
'Fahrenheit'.
It issues an error if x is not a number, or if the number of
arguments actually passed (nargs) is not 2, or if a wrong
conversion rule has been passed (elif clause).
| > convert := proc(x :: number, rule) is > if nargs <> 2 then > error('need two arguments') > elif not(rule in {'C', 'F'}) then > error('incorrect second argument') > else > case rule > of 'C' then > # convert Fahrenheit to Celsius > return (x - 32) * 5/9 > of 'F', 'Fahrenheit' then > # convert Celsius to Fahrenheit > return x * 9/5 + 32 > else > error('unknown rule') > esac > fi > end; > convert(4, 'F'): 39.2 |
Graphics
Agena includes all the basic tools to plot points, lines, circles, ellipses, rectangles, arcs. etc., to control image size, and colours. Plots can be displayed on screen (X11 and Windows) and stored to GIF, PNG, JPEG, FIG, or PostScript files.
| > import gdi alias; |
The plotfn function draws one or more graphs of functions in one real, optionally along with the axes plotted in a user-defined colour. There are various other options which can be set with the setoptions function and which will apply to all graphs produced in a session: the window resolution, the colour map, the line thickness, and background colour. Of course, the user may override some or all options for a specific plot.
| > plotfn([ << x -> x*sin(x)
>>, << x -> cos(x) >>], -5, 5, -2, 2, > colour=['red', 'cyan'], linestyle=[1, 3]); |

Some other examples with a fractals package that uses gdi functions:
| > import fractals alias; > draw(mandel, -0.5, 0, 1.5, map='topo.map', iter=255, res=640:480); |
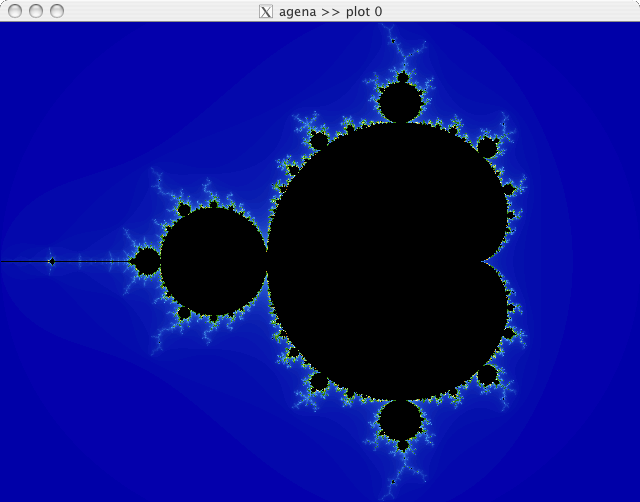
Mandelbrot Set on Mac OS X
Tables
Data types are numbers, booleans, strings, tables, pairs, sequences, and Cantor sets.
Tables can represent simple arrays.
| > a := [10, 11, 12]; |
The first entry:
| > a[1]: 10 |
Change an entry:
| > a[3] := 2; |
Add a new entry with any key:
| > a[5] := 15; > a: [1 ~ 10, 2 ~ 11, 3 ~ 2, 5 ~ 15] |
Tables can also be used to create records:
| > create table people; > people['Donald'] := 'Duckburg'; |
A synonymous notation is:
| > people.Darkwing := 'St. Canard'; > people: [Darkwing ~ St. Canard, Donald ~ Duckburg] |
Cantor Sets
Cantor sets are collections of elements with each element included only once and where order does not matter, so:
| > {1, 2, 2} = {2,
1}: true |
Agena's Cantor sets store elements much more efficiently by consuming 40 % less memory than ordinary tables do; they are very useful in a variety of applications, for example in phonetics to store word lists. All Cantor set operations have been built into the kernel for maximum performance: unions, intersections, difference sets, and subsets.
| > A := {1, 2, 2, 3}; B := {3, 4, 5}; > # all the elements in A that are also part of B > A intersect B: {3} |
You may add or delete one or more elements into or from a set:
| > insert 4, 5 into A; > A: {2, 3, 1, 4, 5} |
The in operator can be used for fast lookups of elements:
| > # test whether an element is part of a set > 5 in A: true |
Strings
You do not have to write functions in order to use Agena's capabilities. Instead, you may execute various statements interactively at the prompt, as well. If you would like to split a text into its words, just enter:
| > beowulf := 'Men ne cunnon hwyder helrunan hwyrftum
scrişağ'; > beowulf split ' ': seq(Men, ne, cunnon, hwyder, helrunan, hwyrftum, scrişağ) |
The above statement creates a sequence of strings. Now we convert all words in the sequence from lower to upper case. The system variable ans always holds the result of the last computation performed:
| > map(<< x -> upper(x) >>,
ans): seq(MEN, NE, CUNNON, HWYDER, HELRUNAN, HWYRFTUM, SCRIŞAĞ) |
Alternatively, use the @ operator, which is quite faster:
| > << x -> upper(x) >> @
(beowulf split ' '): seq(MEN, NE, CUNNON, HWYDER, HELRUNAN, HWYRFTUM, SCRIŞAĞ) |
The number of words in the sequence is:
| > size(ans): 7 |
If we translate this Old English sentence taken from the Beowulf saga to New English, we get:
| > replace(beowulf, seq('Men':'Men', 'ne':'do
not', > 'cunnon':'know', 'hwyder':'where', 'helrunan':'villains', > 'hwyrftum':'\b', 'scrişağ':'go')): Men do not know where villains go |
Remember Tables
Procedures can remember their results. Recursive procedures are quite slow:
| > fib := proc(n)
is > assume(n >= 0 and not(float(n))); > if n < 2 then > return 1 > else > return fib(n-2) + fib(n-1) > fi > end; |
The 30th Fibonacci number takes 5.76 seconds to compute on a Sparc Sun Blade 150 with 550 MHz:
| > t := time(); print(fib(30),
time()-t); 1346269 5.76 |
But if you create a remember table for the procedure, the results computed during recursion are stored to an internal table and can be accessed immediately.
| > rtable.remember(fib, []); |
Now the procedure will be much faster and the time needed to complete the computation cannot even be measured.
| > t := time(); print(fib(30),
time()-t); 1346269 0 |
You can also assign predefined results to a procedure. Let us define a factorial function fact(n) = n! :
| > fact := proc(n :: number) is > if float(n) then # is n not an integer ? > return undefined > else > return exp(lngamma(n+1)) > fi > end; |
Now register eleven precomputed results with this function so that fact does not need to compute the result for integral arguments n = 0 .. 10. Note that in this example, 5! is undefined, since this result has been predefined.
| > rtable.defaults(fact, [ > 0~1.0000000000000000e+00, 1.0000000000000000e+00, > 2.0000000000000000e+00,6.0000000000000000e+00, > 2.4000000000000000e+01, undefined, 7.2000000000000000e+02, > 5.0400000000000000e+03, 4.0320000000000000e+04, > 3.6288000000000000e+05, 3.6288000000000000e+06]); > fact(11): 39916800 > fact(5): undefined |
Of course, both features can be mixed. You can define predetermined values and enter results of actual function calls into a remember table for instant access.
A simple way to switch on the remember table functionality is to pass the feature reminisce statement right after the is keyword in a procedure definition.
| > fib := proc(n)
is > feature reminisce; > if n < 2 then > return 1 > else > return fib(n-2) + fib(n-1) > fi > end; > fib(30): 1346269 |

